Objective:
- Short-term supply-chain effects of different containment strategies across countries and industry sectors to inform ongoing efforts to contain COVID-19 and to reveal more generally how pandemic-related economic losses will be distributed along global supply chains
Case:
Methodology:
- CGE:
- production: $x_i = f(for all p, z_i^p; va_i)$
- $x_i$ is the output of the firm in monetary values;
- $p$ denotes the type of intermediate products
- $z_i^p$ is the intermediate products used in production
- $va_i$ is the primary inputs such as labor, capital and natural resources
- Leontief production function that not allow substitution between inputs: $x_i = min(for all p, \frac{p_i^p}{a_i^p}; \frac{va_i}{b_i})$
- $a_i$ is the input coefficient $a_i^p = \frac{\overline{x}_i}{\overline{z}_i^p} $
- Labor supply constraints: $x_i^L(t) = (1-\gamma_i^L(t)) \times \overline{x}_i$
- $\gamma_i^L(t)$ is the proportion of labor that is unavailable at time step $t$
- Supply constraints: $x_i^p (t) = \frac{S_i^P(t-1)}{a_i^p}$
- Maximum supply capacity: $x_i^{max}(t) = min(x_i^L (t): for all p, x_i^p(t))$
- Allocation module
- Demand module
Data Source: Open
- Global trade analysis project: Input-output table
Findings:
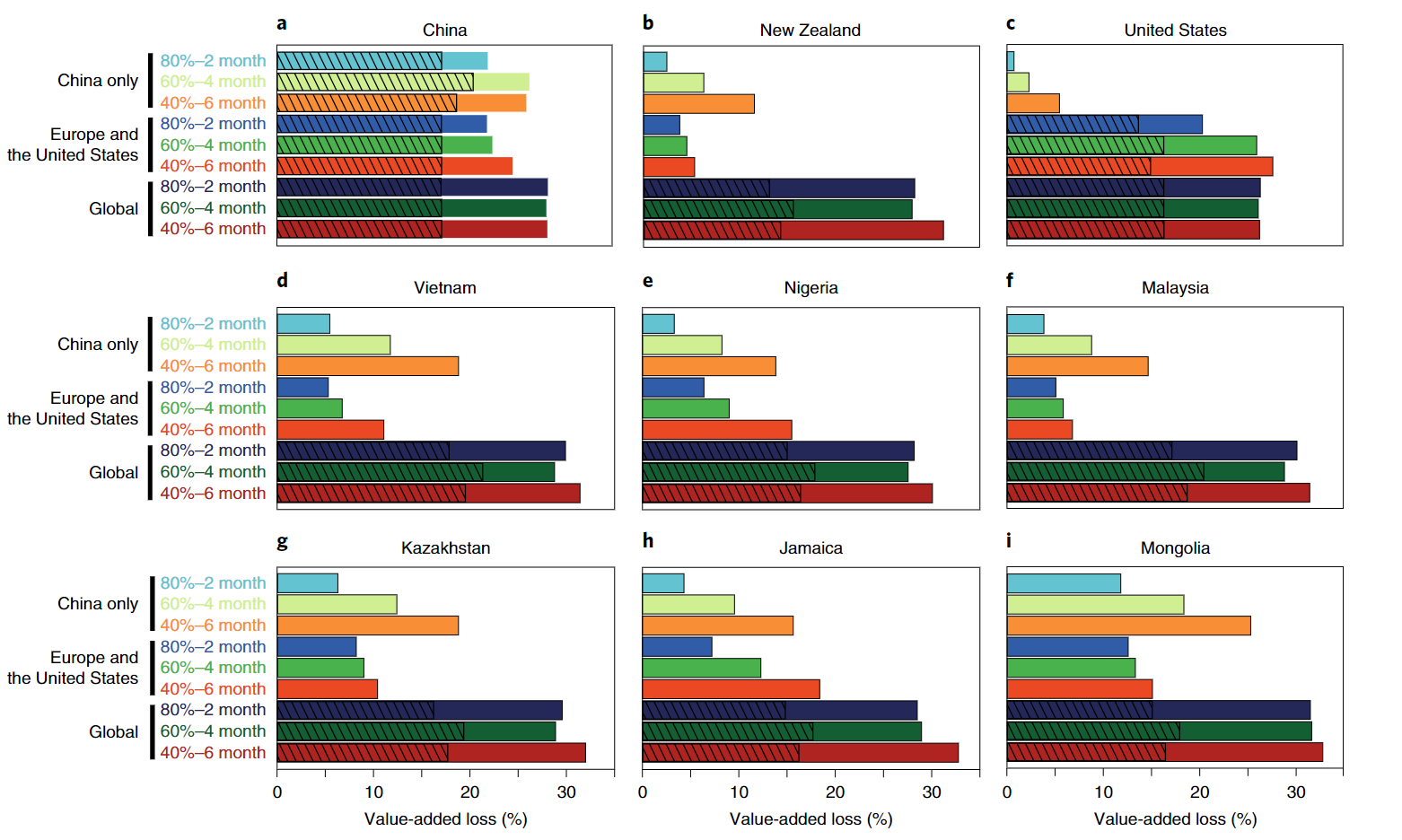
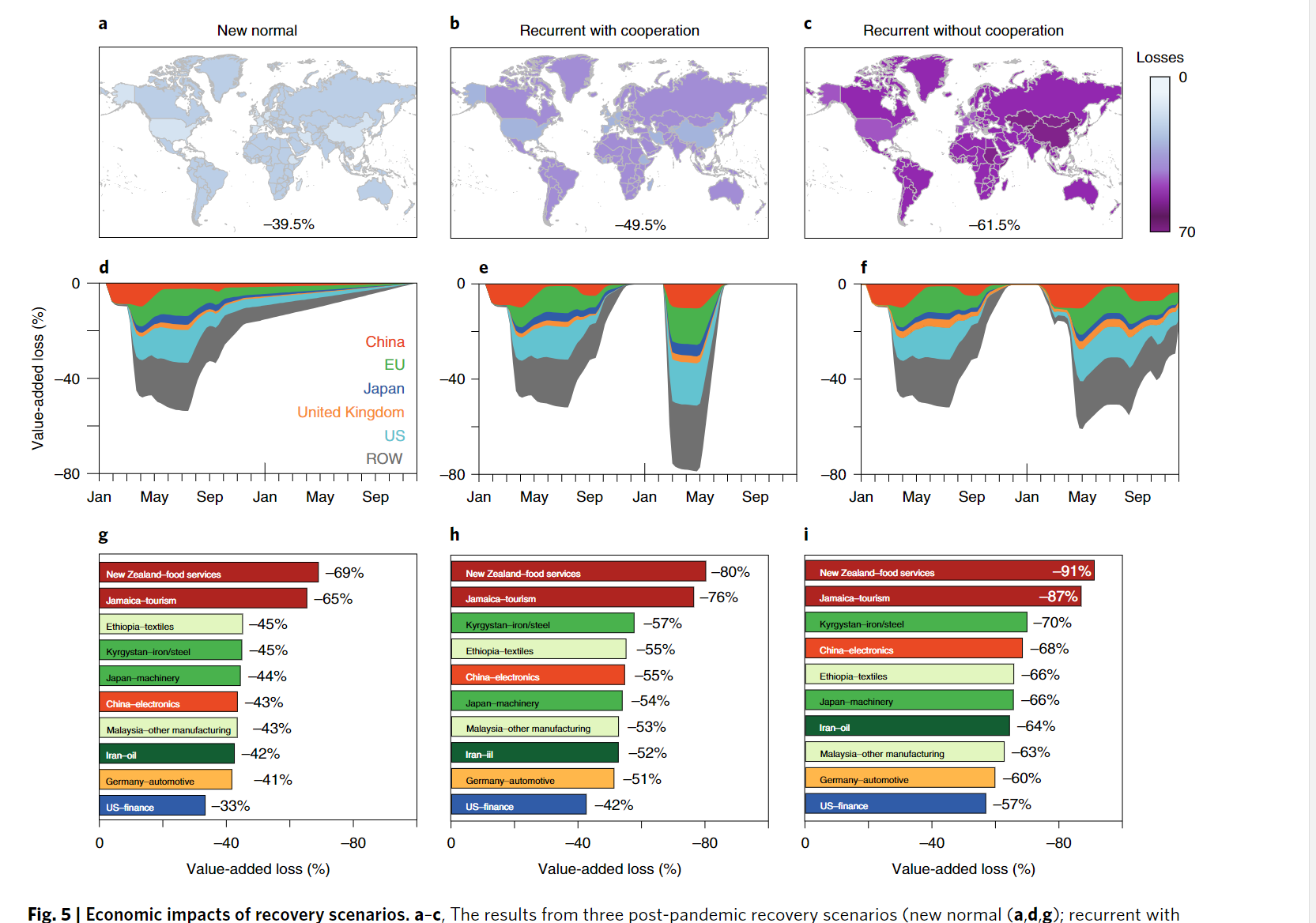
- Global cost of the pandemic depends foremost on the number of affected countries, and then on the required duration of lockdown policies
- The strictness of these policies is comparatively less important
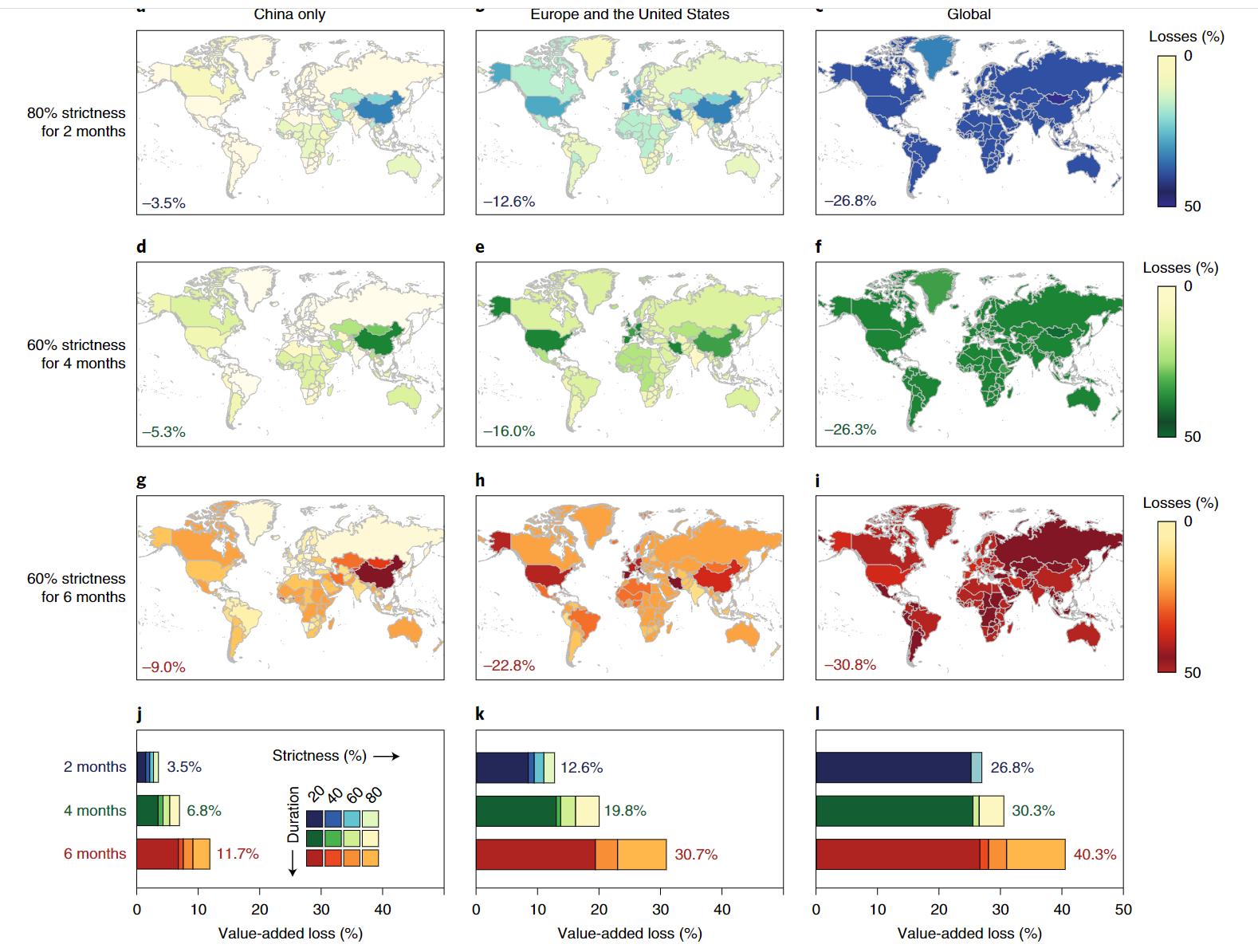
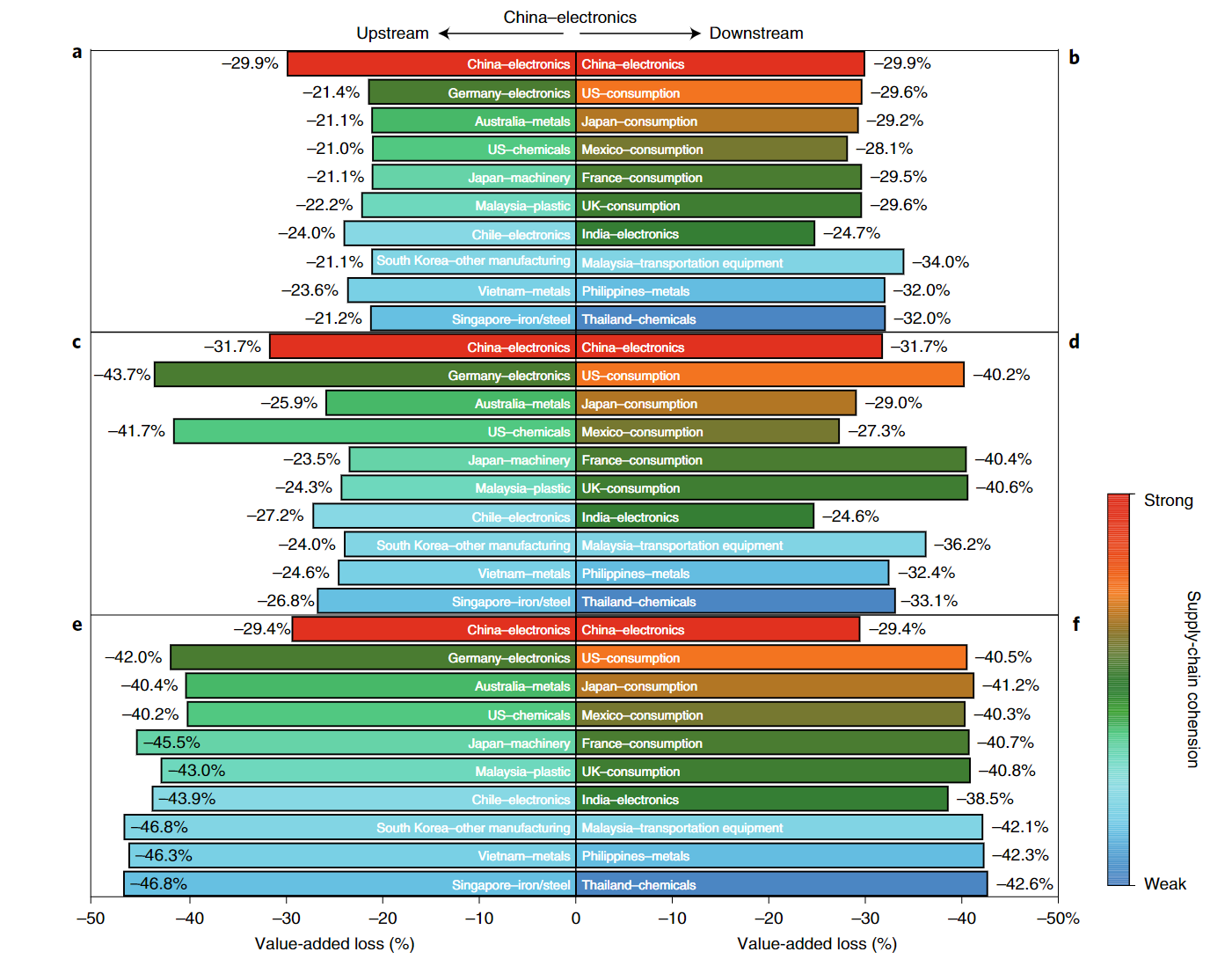
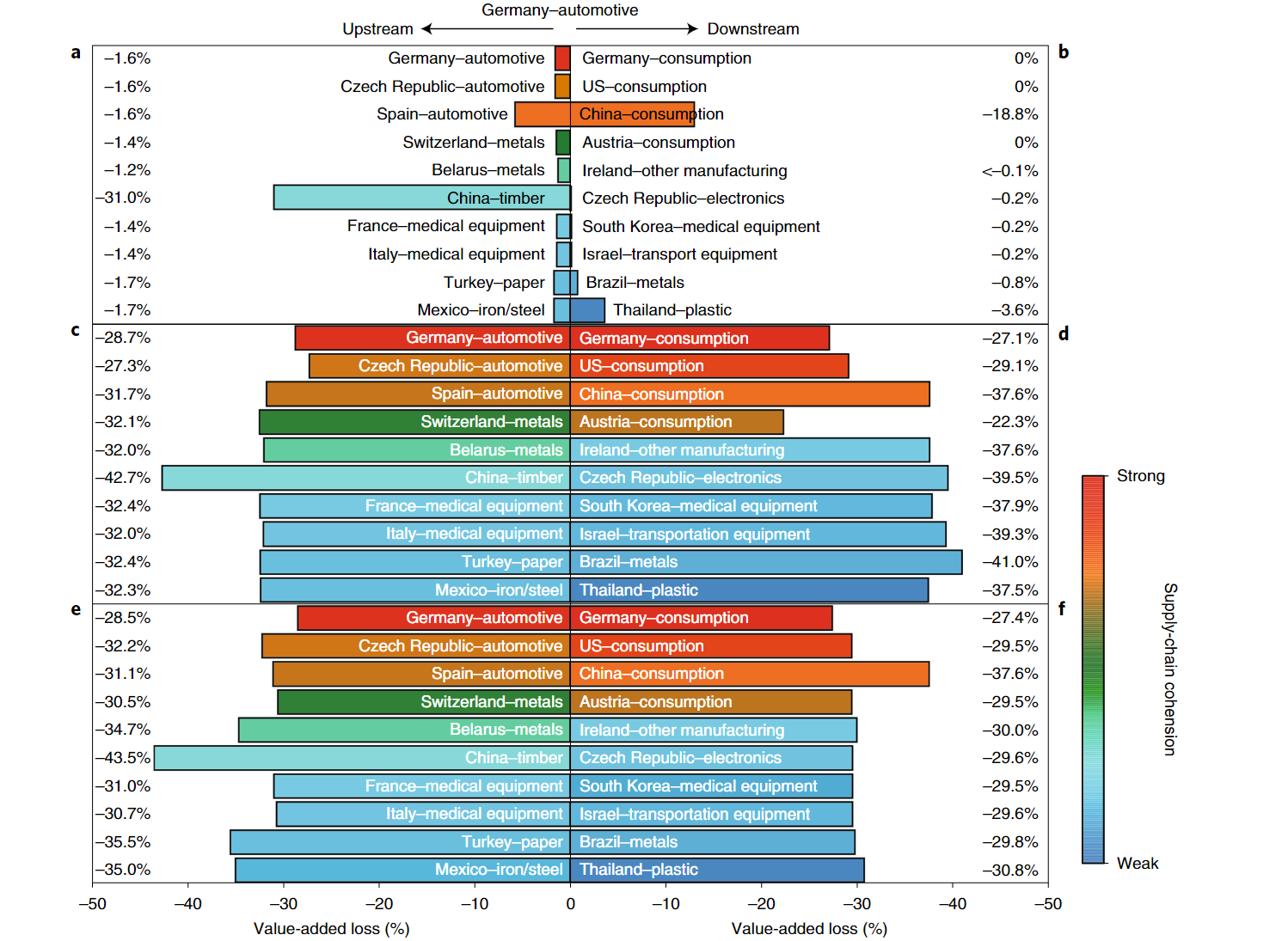
- The importance of propagation through global supply chains-even countries that are not directly affected by the virus experience large losses, and low- and middle-income countries are more vulnerable to indirect effects
Coding Reference:





