Understanding log regression

log-log regression

• Using natural logs for variables on both sides of the OLS equation is called a log-log model. This model is handy when the relationship is non-linear in parameters.

• In principle, any log transformation can be used to transform a model that;s a nonlinear in parameters into a linear one

• Consider a basic function: $Y_i = \alpha X_i^{\beta}$
• If you take the natural log of both sides: $ ln Y_i = ln \alpha + \beta ln X_i $
  • $ln \alpha$ is treated as the intercept
  • The model ends up with: $ln Y_i = {\beta}_0 + {\beta}_1 ln X_i $
• Interprete the coefficients:
  • $\frac{\delta Y}{Y} = {\beta}_1 \frac{\delta X}{X}$
  • The term on the right-hand side is the percentage change in $X$; and the term on the left-hand side is the percentage change in Y, so
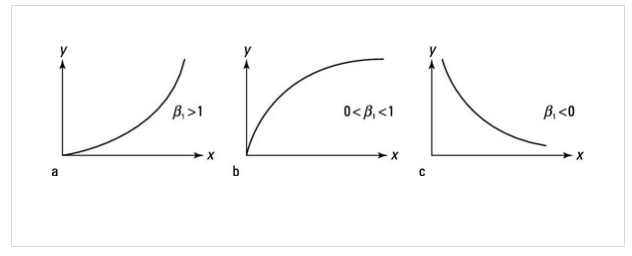
  • ${\beta}_1$ measures the elasticity

semi-log regression

• For the equation: $ ln Y_i = \alpha + \beta X_i $
  • $\frac{\delta Y}{Y} = \delta X$
  • The term on the right-hand side is the unit change in $X$; and the term on the left-hand side is the percentage change in Y,
• For the equation: $ Y_i = \alpha + \beta ln X_i $
  • $\delta Y = \frac{\delta X}{X}$
  • The term on the right-hand side is the percentage change in $X$; and the term on the left-hand side is the unit change in Y,

Marginal effects

• However, the percentage change ((semi-)elasticity) can only capture the correlation between $X$ and $Y$. It can’t represent the importance of indicators
• If we want to measure the importance, The elasticity should be transformed into marginal impacts
  • $Margin = X * elasticity$